Galilei und die neue Wissenschaft:
Experiment und Mathematik
Von Josef Honerkamp
Die Erkenntnis, dass es in einem Meer von Mystik und Dialektik immerhin noch die Möglichkeit gibt, die Wahrheit von Aussagen auf eine andere Aussage zu übertragen, hat mich in meiner Jugend, als mir dieses so richtig bewusst geworden war, sehr umgetrieben.
Wozu konnte man das nicht alles benutzen! Man könnte ja so eine Art logischer Ordnung zwischen Aus- sagen herstellen, in der klar wird, welche Aussagen aus welchen anderen Aussagen jeweils folgen. Man könnte von wahren Aussagen starten und darauf ein ganzes Gedankengebäude errichten, das nur aus wahren Aussagen besteht. Aber – mit welchen Aussagen kann man anfangen? Das war die große Frage.
Die Organisation sicheren Wissens
Solche Gedanken liegen natürlich nahe. In der Tat hatten sie auch schon die antiken Griechen. Aristoteles hatte, wie schon einem früheren Blogbeitrag erwähnt, gezeigt, dass man von den Syllogismen der 1. Form ausgehend, alle anderen Syllogismen ableiten kann. Er hatte damit das Problem, wie man überhaupt zu wahren Aussagen kommt, in der Weise gelöst, dass er die Syllogismen der 1. Form als wahre Sätze betrachtete. Diese waren ja auch unmittelbar einleuchtend. Einige Jahrzehnte später hatte dann Euklid von Alexandria das damalige Wissen über geometrische Flächen und Körper logisch geordnet und damit das erste größere axiomatisch-deduktive Gedankengebäude erstellt. Auch hier musste er zu Beginn einige Sätze als wahr ansehen. Hier schienen diese aufgrund der Anschauung evident zu sein.
In der Begriffslogik und in der Geometrie war also schon ein Modell entwickelt worden, mit dem man die Erkenntnis, dass es einen sicheren Transport von Wahrheit gibt, verwerten konnte. Wie wir aber im letzten Blogbeitrag gesehen haben, hat man erst sehr viel später die logische Basis für die Schlussfolgerungen in der Mathematik verstanden. Vorher galten diese als „unmittelbar einleuchtend“. Man machte dabei etwas richtig, konnte es nur nicht genau begründen; ja, man wusste nicht einmal, dass es da etwas zu begründen gab. Erst später sollte es nicht mehr reichen, dass einem etwas „unmittelbar einleuchtet“.
So war damals die Mathematik das einzige Gebiet, in dem man mit sicherem Wissen umgehen und auch praktische Probleme lösen konnte. Im 20. Jahrhundert ist nun die mathematische Logik dazu gestoßen. Zunächst war diese nur für theoretische Fragen interessant wie z.B. für das Studium der Grundlagen der Mathematik. Heute ist sie aber auch Grundlage für viele Algorithmen, die für die Extraktion und Gewinnung von Wissen in Rahmen der „künstliche Intelligenz“ entwickelt werden.
Die Mathematik blieb also über all die früheren Jahrhunderte ein unerreichtes Vorbild für die Organisation sicheren Wissens. Man hatte durchaus versucht, eine ähnliche Strenge der Argumentation in Philosophie und Ethik einzuführen. Solche Ansätze waren aber alle im Sand verlaufen (siehe Wikipedia: Mathesis universalis). Waren es die falschen Gebiete für eine Strenge der Gedankenführung nach Art der Mathematisierung gewesen?
Heute sehen wir, wie viele Gebiete der empirischen Wissenschaften immer stärker mathematisiert werden. Galileo Galilei war es, der die ersten Schritte dazu in der Naturforschung machte. Er hat als erster ein Ergebnis eines physikalischen Experimentes in der Sprache der Mathematik beschrieben. Dabei erkannte er durchaus die Tragweite dieser Verknüpfung von Mathematik und Experiment, er sah sofort, welch eine Revolution eine Mathematisierung für das damalige Verständnis von Wissenschaft darstellt. So sprach er von einer „neuen Wissenschaft“, die er begründet habe. Sein Satz „Das Buch der Natur ist in der Sprache der Mathematik geschrieben“ zeugt davon genauso wie auch die Passage seines Briefes an den toskanischen Staatssekretär Vinta im Jahre 1610: „Daher erlaube ich mir, das eine neue Wissenschaft zu nennen, die von ihren Grundlagen angefangen von mir entdeckt worden ist.“
Galilei griff damit den Gedanken der Pythagoreer wieder auf, aber in einer ganz neuen Weise. Er sah auch, dass es eine Ordnung, also Regelmäßigkeiten in der Natur gibt, die sich in mathematischen Beziehungen ausdrücken lassen, und hatte auch durch sein Studium der Euklidschen Geometrie die Strenge der mathematischen Schlussfolgerungen kennen gelernt. Er erkannte aber auch, dass man die Natur durch Experimente „befragen“ muss, um diese Ordnung zu entdecken. Nicht Mathematik allein, nicht Empirie allein, sondern Experiment und Mathematik sind die Pfeiler seiner neuen, strengen Wissenschaft.
Wir kennen alle die Folgen dieser Entdeckung, ohne diese wäre unsere Welt heute eine völlig andere. Irgendwann aber musste wohl diese „neue Wissenschaft“ entdeckt werden; zu nahe stehen sich Natur und Mathematik – besser gesagt: Natur und Logik.
Wann ist eine Implikation wahr?
Warum spielt Empirie, warum spielen „Befragungen“ der Natur in Form von Experimenten eine solch bedeutsame Rolle, wenn man sich eine Theorie nach dem Vorbild der Euklidschen Geometrie, also als axiomatisch-deduktives System wünscht? Schauen wir uns deshalb den Modus ponens als Prototyp eines logischen Schlusses noch einmal an:
A, A → B ⊨ B.
Um auf eine Aussage schließen zu können, die unanfechtbar wahr ist, müssen die Prämissen A und A → B wahr sein. Es gibt eine Aussage, nämlich A, die in beiden Prämissen vorkommt. Die Implikation bildet die Brücke zu einer neuen Aussage, nämlich B, auf die dann geschlossen wird. Solche „Brücken“ muss es in jeder Schlussregel geben, denn aus Aussagen, die völlig unabhängig neben einander stehen, kann nichts geschlossen werden. Auch die Syllogismen besitzen ja jeweils einen Mittelbegriff, der in beiden Prämissen vorkommt.
Eine wahre Implikation A → B bedeutet, dass A hinreichend ist für B: Stets, wenn A, so B. Wo ist das der Fall?
Wir können wahre Implikationen finden, wenn wir die Natur befragen. Wir erhalten dann z.B. folgende Antworten: „Wenn ich einen Ball in die Luft werfe, dann fällt er zu Erde,“ oder „Wenn in einem Draht ein elektrischer Strom fließt, dann existiert ein Magnetfeld in seiner Umgebung.“ Die Experimentalphysiker sind also Lieferanten wahrer Implikationen, die wir dann auch als Naturgesetze formulieren.
Wahre Implikationen können wir auch finden, wenn wir z.B. die Aussage „Alle Griechen sind Menschen“ umformen in
„Wenn x ein Grieche ist, dann ist x ein Mensch“.
Hier haben wir die Begriffe „Griechen“ und „Menschen“ so gebildet, dass die Implikation wahr ist. Die Aussage wird also dadurch wahr, dass wir die Begriffe entsprechend bilden.
Dann sind wir aber schon am Ende. Für alle anderen Implikationen ist wohl der dialektische Schluss zuständig, d.h. hier gehört eine Implikation zu der Kategorie von Sätzen, über die Aristoteles gesagt hat:
Glaubwürdig sind Sätze, wenn sie von Allen, oder von den Meisten oder von den weisen Männern und zwar bei Letzteren von allen, oder von den meisten oder von den erfahrensten und glaubwürdigsten anerkannt werden.
Wir können noch hinzufügen: Und das, was von den „weisen Männern“ anerkannt wird, hängt auch noch von der Zeit ab. Denken wir nur an die Gesetze der Rechtwissenschaft, z.B. an das Gesetz §1356 des BGB, das bis 1977 noch lautete: „Die Frau führt den Haushalt in eigener Verantwortung. Sie ist berechtigt, erwerbstätig zu sein, soweit dies mit ihren Pflichten in Ehe und Familie vereinbar ist.“
Wenn es um Regelungen für das menschliche Zusammenleben geht, um Moral, Sitten und Gebräuche, ja, um alles, was uns die Natur nicht sagt, kann es keine allgemein akzeptierbaren wahren Implikationen geben. Wir sind auf den dialektischen Schluss verwiesen und damit auf ein Verhandeln darüber, welche Implikationen denn als wahr gesetzt werden sollen. Hier können wir also Wahrheit nur „setzen“, nicht finden.
Die Folge davon ist, dass die Aussagen der Naturwissenschaften universell gelten, es aber unzählige Religionen und Rechtssysteme gibt. In den Naturwissenschaften gibt es zwar auch eine Veränderung im Laufe der Zeit. Diese ist aber, wie wir in späteren Blogbeiträgen sehen werden, eine Art von Evolution, ein „Finden vom immer besseren“ Grundannahmen aufgrund von stets neuen Entdeckungen über das Verhalten der Natur.
Einige Zeit hat man geglaubt, dass sich Regeln für das menschliche Zusammenleben auch aus der Natur des Menschen ablesen ließen. Eine solche Naturrechtslehre kann für verschiedenste Ideologien nutzbar gemacht werden. Letztlich sind es immer die „weisen Männer“, welche die Sätze, welche eigentlich nur für einige glaubwürdig erscheinen, allgemein als wahr dekretieren. Die katholische Kirche hält heute noch an dieser Lehre fest. Seit Jahrhunderten spricht man aber von einem „naturalistischen Fehlschluss“, wenn man vom „Sein“ auf das „Sollen“ schließt. Eine Implikation, die Aussagen über das Sein mit einer Aussage über das Sollen verknüpft, ist aus der Natur nicht ablesbar. Wir verdanken dem Philosophen David Hume (1711 bis 1776) die erstmalige explizite Formulierung dieser Einsicht.
Die neue Wissenschaft des Galileo Galilei
Das „heiße“ Thema der Naturforschung zu Zeiten Galileis war die Bewegung. In seinem Werk „Discorsi“ heißt es:
Nichts ist älter als die Bewegung, und über dieselbe gibt es weder wenig noch geringe Schriften der Philosophen. Dennoch habe ich deren Eigentümlichkeiten in großer Menge, und darunter sehr wissenswerte in Erfahrung gebracht.
Die Bewegung war ja schon Thema bei den Vorsokratikern gewesen. Aristoteles hatte verschiedene Klassen von Bewegungen unterschieden und dabei für jede eine besondere Erklärung gefunden. Die Bewegung ist nun einmal das Phänomen, das uns am unmittelbarsten begegnet, das man aber auch am Himmel als Gang der Gestirne beobachten kann. Wenn man überhaupt etwas von der Natur lernen wollte, musste man wohl zunächst die Bewegung „verstehen“.
Was für ein Experiment war das nun, mit dem Galilei die Bewegung studierte, und welche Form von Mathematik wandte er zur Beschreibung der Ergebnisse an? Wie Galilei das Problem anging, ist bemerkenswert und symptomatisch für den Gang der modernen Wissenschaft. Er richtete nicht den Blick auf „das Ganze“ wie die Vorsokratiker es taten, suchte auch keine allgemeine Übersicht zu erstellen wie Aristoteles, sondern fing es „im Kleinen an“. Er ließ eine kleine, glatt polierte Kugel eine schiefe Ebene, d.h. ein schräg gestelltes schmales Holzbrett herunterrollen, in das er eine Rinne eingegraben war – ein Kinderspiel in heutigen Zeiten.
Allein diese Wendung des Blicks zeugt schon von der Unabhängigkeit seines Denkens, wie sie einem Genie eigen ist. Noch zu Goethes Zeiten galt es für Philosophen, über das nachzudenken, „was die Welt im Innersten zusammenhält“, und Faust hat nur Spott für Mephistopheles übrig, wenn er um die Menschen kämpft: „Du kannst im Großen nichts verrichten, und fängst es nun im Kleinen an“. Religionen kennen nur diese Frage nach „dem Großen“.
Eigentlich hat Galilei damit die Fährte von Xenophanes wieder aufgenommen. Wenn man darauf vertraut, dass es möglich sein wird, „suchend das Bessere zu finden“, schätzt man auch „kleine Erfolge“ bei der Suche nach Erkenntnissen; man sucht eine Vorlage, auf der man aufbauen kann. So funktioniert die moderne Wissenschaft, die moderne Technik. Deshalb gibt es Forschung und Entwicklung.
Galilei musste nun bei jedem Rollen der Kugel Zeiten und Wegstrecken messen. Wie er insbesondere eine Zeiteinheit festlegen konnte, in dem er sein Gespür für einen gleichmäßigen Takt bei einem Lied ausnutzte, ist ausführlich in (Fölsing, 1983, p. 177ff) beschrieben. In seinen Aufzeichnungen berichtet er: „ … bei wohl hundertfacher Wiederholung fanden wir stets, dass die Strecken sich verhielten wie die Quadrate der Zeiten, und dieses für jede Neigung der Ebene, das heißt der Rinne, in dem die Kugel lief.“(Discorsi, nach (Fölsing, 1983, p. 174)).
Galilei formulierte das Ergebnis in Form von Proportionen, Verhältnissen, wie es damals üblich war und wie man es anders noch nicht gelernt hatte. Zeitabschnitte und Wegstrecken waren ja Größen unterschiedlicher Dimension, und man hatte noch nicht verstanden, wie man solche Größen direkt in Beziehung setzen kann. Deshalb schrieb er sein Ergebnis nicht in der Form auf, in der die Wegstrecke proportional zum Quadrat der benötigten Zeit auf, sondern als Gleichheit der Verhältnisse von zwei Strecken und zwei Quadraten entsprechender Zeiten. In einem Graphen, in dem die Zeiten gegen die Wegstrecken aufgetragen sind, stellt sich das als eine Halbparabel dar, etwa so, wie man sie in der Tat im Dialogo Quarto des Discorsi Galileis bei der Diskussion geworfener Körper findet (Abb. 1).
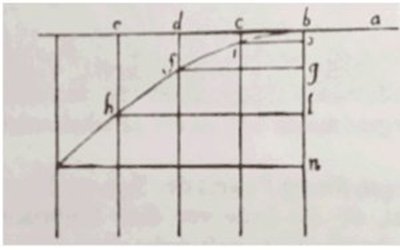
Galilei war zudem von einem Ingenieur und Geometer Ostilio Ricci in die Schönheit und Stringenz der “Geometrie” des Euklids eingeweiht worden. Er war damit auch schon von dem Gedanken „infiziert“, seine experimentellen Aussagen logisch ordnen zu müssen. Er suchte somit auch ein Prinzip, aus dem alle diese Aussagen herleitbar sind. Dabei geriet er allerdings auf eine falsche Fährte. Vier Jahre später konnte er diesen Irrtum korrigieren (Fölsing, 1983, p. 175ff). Eine solche „Theorie“ für eine Fallbewegung wäre ohnehin bald obsolet gewesen. Er konnte nicht ahnen, dass am Ende seines Jahrhunderts eine Theorie entstehen sollte, die alle Bewegungen am Himmel und auf der Erde von einigen wenigen Axiomen ausgehend erklären konnte. Seine Fallbewegung wurde darin zu einem kleinen Spezialfall.
Der englische Physiker und Mathematiker Isaac Newton stand bei der Entwicklung dieser Theorie gewissermaßen auf den Schultern Galileis. Das erste Axiom in dieser Theorie stützte sich nämlich auf eine Hypothese Galileis, auf die dieser bei seinen Fallexperimente geführt worden war. Es war die Hypothese, dass auf einer horizontalen Ebene die rollende Kugel ihre Geschwindigkeit „im Prinzip“ nicht ändert.
Eine solche Bewegung nennen wir heute geradlinig-gleichförmig, d.h. einer geraden Linie folgend und gleichbleibend in der Geschwindigkeit. Diese stellt nun einen Zustand der Kugel dar, bei dem nichts „erzwungen“ werden muss. Wenn man dieses Prinzip richtig verinnerlicht, kommt man vielleicht auf die Frage, wie sich denn diese Bewegung verändert, wenn man etwas „erzwingt“. Diese Hypothese Galileis muss also wohl eine Steilvorlage für Isaac Newton gewesen sein, und steht somit nicht ohne Grund am Anfang seiner Theorie. In der Praxis kommt die Kugel im Experiment Galileis natürlich zur Ruhe. Dafür sorgt die Reibung der Kugel an der Oberfläche.
Dieses Abebben der Bewegung durch die Reibung ist für Aristoteles in diesem Kontext die natürliche, eigentliche Bewegung, sie ist ein Prozess. Mit „Zwang“ kann sie aufrechterhalten werden. Die Ruhe ist für die Aristoteliker wie auch für die Vorsokratiker ein ganz besonderer Zustand, „wesensmäßig“ verschieden von einer Bewegung.
Bei Galilei ist in diesem Kontext die geradlinig-gleichförmige die natürliche, eigentliche Bewegung, sie ist ein Zustand. Durch äußere Umstände wie Reibung kann sie zur Ruhe kommen. Ruhe ist nur ein spezieller Zustand dieser Art, gewissermaßen das Nullelement der Klasse der geradlinig-gleichförmigen Bewegugen. Diese Einsicht steht am Anfang der modernen Physik.
Mit welchen Aussagen kann man bei der Formulierung eines axiomatisch-deduktiven Systems anfangen? Die Antwort auf diese Frage lag für eine Theorie der Bewegung, die Newton dann entwickelte, nahe: Die Einsicht Galileis musste wohl am Anfang einer Theorie der Bewegung stehen.
Schauen wir uns an, welche Aussagen in dieser Theorie, aber auch welche noch in weiteren physikalischen Theorien an den Anfang gestellt worden sind. Wir werden sehen, dass das auf höchst unterschiedliche Weise geschah. Verschaffen wir uns aber erst einmal im nächsten Blogbeitrag einen Überblick über diese Theorien.

Keine Kommentare:
Kommentar veröffentlichen